4.2

Complements, Intersections, and Unions

Learning Objectives

Upon completion of this section, you should be able to

• Solve probability applications using the complement rule.
• Find the probability when there is a union of two events.
• Find the probability when there is an intersection of two events.

Complement of an Event

Now let us examine the probability that an event does not happen. As in the previous section, consider the situation of rolling a six-sided die and first compute the probability of rolling a six: the answer is P(six) = 1/6. Now consider the probability that we do not roll a six: there are 5 outcomes that are not a six, so the answer is $P\left(\text{not a six}\right)=\frac{5}{6}$ .

Notice that  $P(\text{six})+P(\text{not a six})=\frac{1}{6}+\frac{5}{6}=\frac{6}{6}=1$

This is not a coincidence. When you think of the events "E" and "Not E" these two must capture all the outcomes in the sample space into two different sets. The probability must then add up to 1 as there are no other collection of outcomes left from the sample space.

Intersection of events

As we continue our study in probability we need a way to describe what outcomes two events have in common. We can do this by bringing in new notation (as shown below) and call it an intersection.

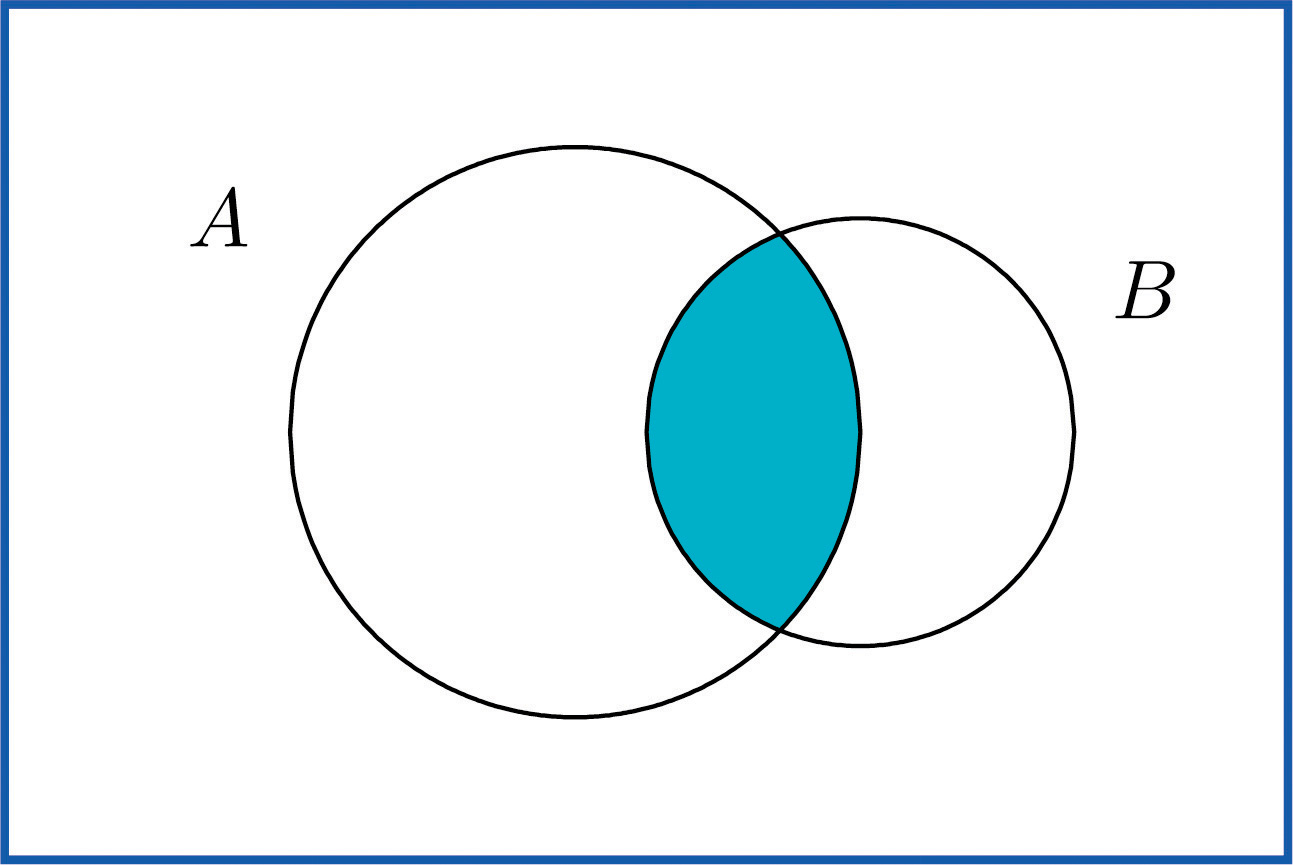
To say that the event $A\cap B$ occurred means that on a particular trial of the experiment both A and B occurred. A visual representation of the intersection of events A and B in a sample space S is given below "The Intersection of Events ". The intersection corresponds to the shaded lens-shaped region that lies within both ovals.

Please be aware that certain images and Google documents may not be properly viewed on mobile devices.

For A and B to have no outcomes in common means precisely that it is impossible for both A and B to occur on a single trial of the random experiment. This gives the following rule.

Any event A and its complement $A^C$ are mutually exclusive, but A and B can be mutually exclusive without being complements.

Union of Events

Now that we have a way to talk about what outcomes two events have in common we will look at how we describe the total outcomes in two or more events. These outcomes do not have to sit within both (or many) events to be part of that group.

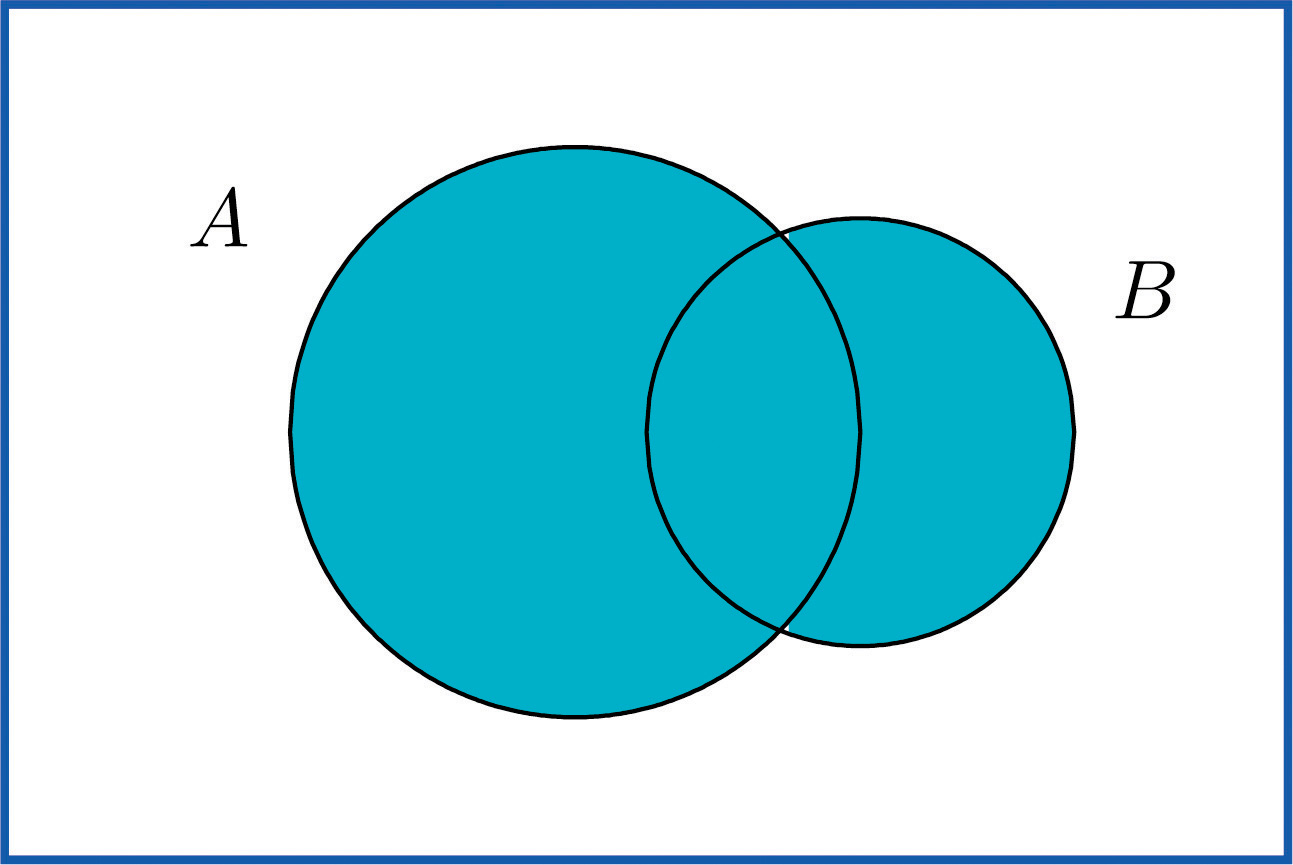
To say that the event $A\cup B$ occurred means that on a particular trial of the experiment either A or B occurred (or both did). A visual representation of the union of events A and B in a sample space S is given in "The Union of Events." The union corresponds to the shaded region.

Please be aware that certain images and Google documents may not be properly viewed on mobile devices.

The following Additive Rule of Probability is a useful formula for calculating the probability of $A\cup B$ .

The next example, in which we compute the probability of a union both by counting and by using the formula, shows why the last term in the formula is needed.

We will finish this section with an example that shows data given to us in a two-way classification table.

Exercises

1. For the sample space $S=\left\{a,b,c,d,e\right\}$ identify the complement of each event given.
   1. $A=\left\{a,d,e\right\}$
   2. $B=\left\{b,c,d,e\right\}$
   3. S

   Answer

   1. $A^C=\left\{b,c\right\}$

   2. $B^C=\left\{a\right\}$

   3. $S^C=\varnothing$ : This is called the empty set as the complement of the entire smaple space consists of no outcomes.

2. For the sample space $S=\left\{r,s,t,u,v\right\}$ identify the complement of each event given.
   1. $R=\left\{t,u\right\}$
   2. $T=\left\{r\right\}$
   3. $\varnothing$ (the “empty” set that has no elements)

   Answer

   1. $R^C=\left\{r,s,v\right\}$

   2. $T^C=\left\{s,t,u,v\right\}$

   3. The complement would be the entire sample space S

3. The sample space for three tosses of a coin is $$S=\left\{hhh,hht,hth,thh,htt,tht,tth,ttt\right\}$$ The events H and M are defined below. H: at least one head is observed M: more heads than tails are observed

   Complete the following

   1. List the outcomes that comprise H and all the outcomes that comprise M.
   2. List the outcomes that comprise $H\cap M$ , $H\cup M$ , and $H^C$ .
   3. Assuming all outcomes are equally likely, find P $P\left(H\cap M\right)$ , $P\left(H\cup M\right)$ , and $P\left(H^C\right)$ .
   4. Determine whether or not $P\left(H^C\right)$ and M are mutually exclusive. Explain why or why not.

   Answer

   1. $H=\left\{hhh,hht,hth,thh,htt,tht,tth\right\}$ , $M=\left\{hhh,hht,hth,thh\right\}$

   2. $H\cap M=\left\{hhh,hht,hth,thh\right\}$ , $H\cup M=\left\{hhh,hht,hth,thh,htt,tht,tth\right\}=H$ , $H^C=\left\{ttt\right\}$

   3. $P\left(H\cap M\right)=\frac{4}{8}$ , $P\left(H\cup M\right)=\frac{7}{8}$ , $P\left(H\cup M\right)=\frac{7}{8}$

   4. Mutually exclusive because they have no elements in common.

4. For the experiment of rolling a single six-sided die once the events T and G are defined below. T: the number rolled is three G: the number rolled is four or greater

   Complete the following

   1. List the outcomes that comprise T and G.
   2. List the outcomes that comprise $T\cap G$ , $T\cup G$ , $T^C$ , and ${\left(T\cup G\right)}^C$ .
   3. Assuming all outcomes are equally likely, find $P\left(T\cap G\right)$ , $P\left(T\cup G\right)$ , $P\left({\left(T\cup G\right)}^C\right)$ , and $P\left(T^C\right)$ .
   4. Determine whether or not T and G are mutually exclusive. Explain why or why not.

   Answer

   1. $T=\left\{3\right\}$ and $G=\left\{4,5,6\right\}$

   2. The outcomes are:

      $$\begin{array}{l}T\cap G=\varnothing \\ T\cup G=\left\{3,4,5,6\right\}\\ T^C=\left\{1,2,4,5,6\right\}\\ {\left(T\cup G\right)}^C=\left\{1,2\right\}\end{array}$$

   3. The probabilities are:

      $$\begin{array}{l}P\left(T\cap G\right)=0\\ P\left(T\cup G\right)=\frac{4}{6}\\ P\left(T^C\right)=1-P\left(T\right)=1-\frac{1}{6}=\frac{5}{6}\\ P\left({\left(T\cup G\right)}^C\right)=1-P\left(T\cup G\right)=1-\frac{4}{6}=\frac{2}{6}\end{array}$$

   4. They are mutually exclusive as they share not outcome in common. T consists of only the outcome of 3 and we do not find that in the set of outcomes for G.

5. Confirm that the probabilities in the two-way contingency table add up to 1, then use it to find the probabilities of the events indicated.

   	U	V	W
   A	0.15	0.00	0.23
   B	0.22	0.30	0.10

   1. $P\left(A\right)$ , $P\left(B\right)$ , $P\left(A\cap B\right)$ .
   2. $P\left(U\right)$ , $P\left(W\right)$ , $P\left(U\cap W\right)$ .
   3. $P\left(U\cup W\right)$ .
   4. $P\left(V^C\right)$ .
   5. Determine whether or not the events A and U are mutually exclusive; the events A and V.

   Answer

   1. $P\left(A\right)=0.38$ , $P\left(B\right)=0.62$ , $P\left(A\cap B\right)=0$

   2. $P\left(U\right)=0.37$ , $P\left(W\right)=0.33$ , $P\left(U\cap W\right)=0$

   3. The probability is:

      $$\begin{array}{l}P\left(U\cup W\right)=P\left(U\right)+P\left(W\right)-P\left(U\cap W\right)\\ P\left(U\cup W\right)=0.37+0.33+0\\ P\left(U\cup W\right)=0.770\end{array}$$

   4. $P\left(V^C\right)=1-P\left(V\right)=1-0.30=0.70$ , take note how the complement of V is all of U or W.

   5. $P\left(A\cap U\right)=0.15\ne 0$ , so A and U are not mutually exclusive. $P\left(A\cap V\right)=0$ , A and V are mutually exclusive.

6. Make a statement in ordinary English that describes the complement of each event (do not simply insert the word “not”).
   1. In the roll of a die: “five or more.”
   2. In a roll of a die: “an even number.”
   3. In two tosses of a coin: “at least one heads.”
   4. In the random selection of a college student: “Not a freshman.”

   Answer

   1. Roll a four or less.

   2. Roll an odd number.

   3. No heads

   4. Select a freshman

7. A tourist who speaks English and German but no other language visits a region of Slovenia. If 35% of the residents speak English, 15% speak German, and 3% speak both English and German, what is the probability that the tourist will be able to talk with a randomly encountered resident of the region?

   Answer

   The randomly chosen resident must speak English or German (or both).

   $$\begin{array}{l}P\left(E\cup G\right)=P\left(E\right)+P\left(G\right)-P\left(E\cap G\right)\\ P\left(E\cup G\right)=0.35+0.15-0.03\\ P\left(E\cup G\right)=0.48\end{array}$$
8. The table relates the response to a fund-raising appeal by a college to its alumni to the number of years since graduation.

   Response	Years Since Graduation
   	0–5	6–20	21–35	Over 35
   Responded	120	440	210	90
   No Response	1380	3560	3290	910

   An alumnus is selected at random. Adjoin the row and column totals to the table and use the expanded table to find the probability of each of the following events.
   1. The alumnus responded.
   2. The alumnus did not respond.
   3. The alumnus graduated at least 21 years ago.
   4. The alumnus graduated at least 21 years ago and responded.

   Answer

   1. $P\left(R\right)=\frac{120+440+210+90}{120+440+210+90+1380+3560+3290+910}=\frac{860}{10000}$

   2. $P\left(R^C\right)=1-P\left(R\right)=1-\frac{860}{10000}=\frac{9140}{10000}$

   3. $P\left(\text{at least 21 years}\right)=\frac{210+90+3290+910}{10000}=\frac{4500}{10000}$

   4. $P\left(\text{at least 21 years}\cap \text{R}\right)=\frac{210+90}{10000}=\frac{300}{10000}$

9. Compute the probability of rolling a fair 12-sided die (numbered 1 to 12) and getting a number other than 8.

   Answer

   $P\left(\text{not 8}\right)=1-P\left(\text{roll a 8}\right)=1-\frac{1}{12}=\frac{11}{12}$

10. Referring to the grade table below, what is the probability that a student chosen at random did NOT earn a C?

    	A	B	C	Total
    Male	8	18	13	39
    Female	10	4	12	26
    Total	18	22	25	65

    Answer

    $P\left(\text{Not a C}\right)=1-P\left(C\right)=1-\frac{25}{65}=\frac{40}{65}$

11. Referring to the credit card table below, what is the probability that a person chosen at random has at least one credit card? Answer the question with and without using the complement rule.

    	Zero	One	Two or more	Total
    Male	9	5	19	33
    Female	18	10	20	48
    Total	27	15	39	81

    Answer

    Without Complement Rule: $P\left(\text{at least 1 CC}\right)=\frac{15+39}{81}=\frac{54}{81}$

    With Complement Rule: $P\left(\text{at least 1 CC}\right)=1-P\left(\text{No CC}\right)=1-\frac{27}{81}=\frac{54}{81}$

12. A fair die is rolled twice. Find the follow probabilities:
    1. Showing a 5 on the first roll and an even number on the second roll?
    2. Showing a 5 on the first roll or an even number on the second roll?

    Answer

    Let A be the even of a F1 on first roll and E2 be the event of even on second roll

    1. $P\left(F1\text{ and E2}\right)=\frac{3}{36}$

    2. Use the additive rule:

       $$\begin{array}{l}P\left(F1\text{ or E2}\right)=P\left(F1\right)+P\left(E2\right)-P\left(F1\text{ and E2}\right)\\ P\left(F1\text{ or E2}\right)=\frac{6}{36}+\frac{18}{36}-\frac{3}{36}\\ P\left(F1\text{ or E2}\right)=\frac{21}{36}\end{array}$$
13. Suppose that $P(E)=0.4,P\left(F\right)=0.5$ = .5. From the limited information, find a maximum and minimum value for $P(E\text{ or }F)$ . Make sure to explain your answer for each case.

    Answer

    1. Maximum: 0.90. E and F are mutually exclusive.

    2. Minimum: 0.50. All outcomes in F are also in E.

14. Suppose that $P(E)=0.4,P\left(F\right)=0.5$ = .5. From the limited information, find a maximum and minimum value for $P(E\text{ and }F)$ . Make sure to explain your answer for each case.

    Answer

    1. Maximum: 0.40. All outcomes in F are also in E, but largest intersection can be is F.

    2. Minimum: 0. F and E are mutually exclusive.

15. The probability that you get a raise is 0.68, the probability that you get your own office is 0.41, and the probability that you get a raise and your own office is 0.24. Answer the following:
    1. What is the probability you get a raise or your own office?
    2. What is the probability you do not get your own office?

    Answer

    Let R be the event you get a raise and O be the event you get your own office.

    1. Use the additive rule.

       $$\begin{array}{l}P\left(RorO\right)=P\left(R\right)+P\left(O\right)-P(RandO)\\ P\left(RorO\right)=0.68+0.41-0.24\\ P\left(RorO\right)=0.85\end{array}$$

    2. $P\left(O^C\right)=1-P\left(O\right)=1-0.41=0.59$